CS336-Assignment2
Targets
- Benchmarking and profiling harness
- Flash Attention 2 Triton kernel
- Distributed data parallel training
- Optimizer state sharding
- 代码仓库
Profiling
1.如何测量所写代码的性能?时间和内存两方面
推荐先读读这几篇高质量博客:
-
分析模型训练的性能:https://horace.io/brrr_intro.html
- 课上tile wave博客:https://www.thonking.ai/p/what-shapes-do-matrix-multiplications
- openai 使用triton写softmax的例子:https://openai.com/index/triton/
1.使用手动设置time进行测量:
- 需要进行warm up,让机器先跑几遍,减少开销的误差
- 使用更精确的timeit计时,或者timeit.default_timer()
- 需要使用异步等待GPU完成,torch.cuda.synchronize()
2.使用自动分析的GPU性能工具,这里使用NVIDIA Nsight Systems,命令行工具是nsys,分析各模块:
- 使用nvtx进行标记代码,分析时候可视化更方便,知道具体各模块的性能:
# 用法举例
@nvtx.range("scaled dot product attention") # 装饰器一个函数测量
with nvtx.range("computing attention scores"): # 测量一段代码时间
attention = q @ k.transpose(-1,-2) / d_k ** 0.5
# push 和pop中间是所测量的部分
nvtx.range_push(f"forward pass test {i-4}")
forward_pass_time.append(timeit.timeit(forward_pass_only, number=1))
nvtx.range_pop()
总体可视化界面如下:分为cpu ,cuda hw, threads三部分大体,我们重点看cuda kernel和threads 里标记的nvtx即可
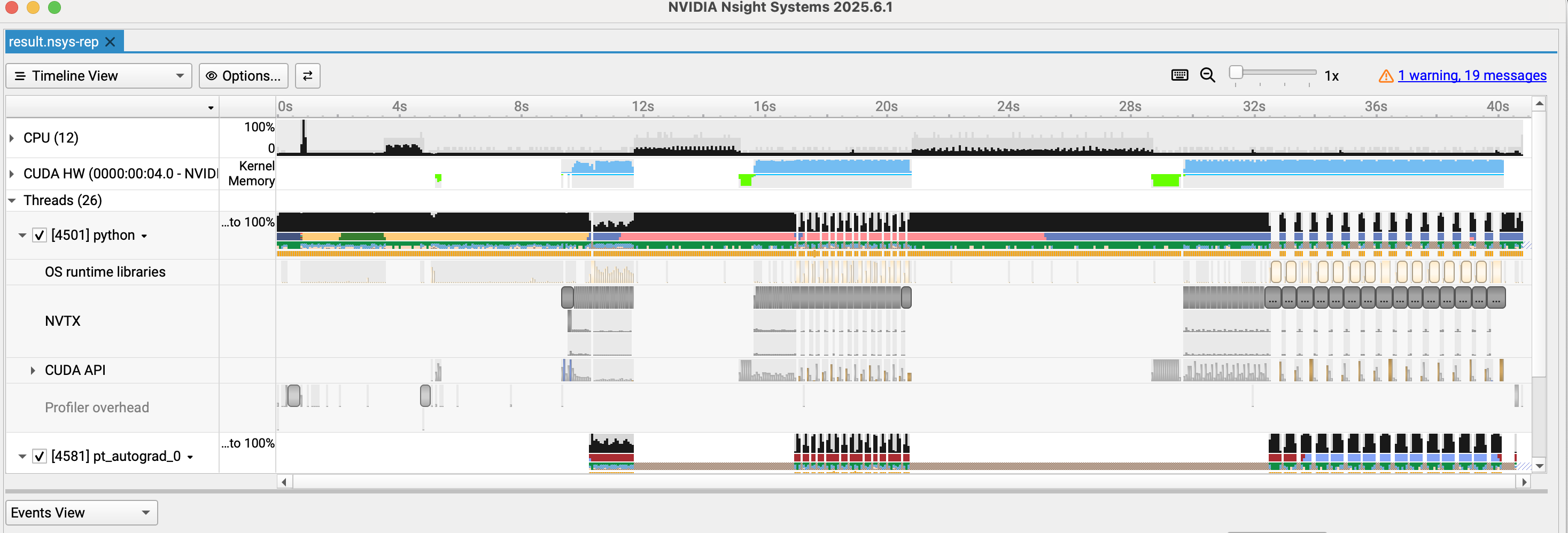
具体的放大部分可以看到每个模块的占用时间和对应调用的kernel:
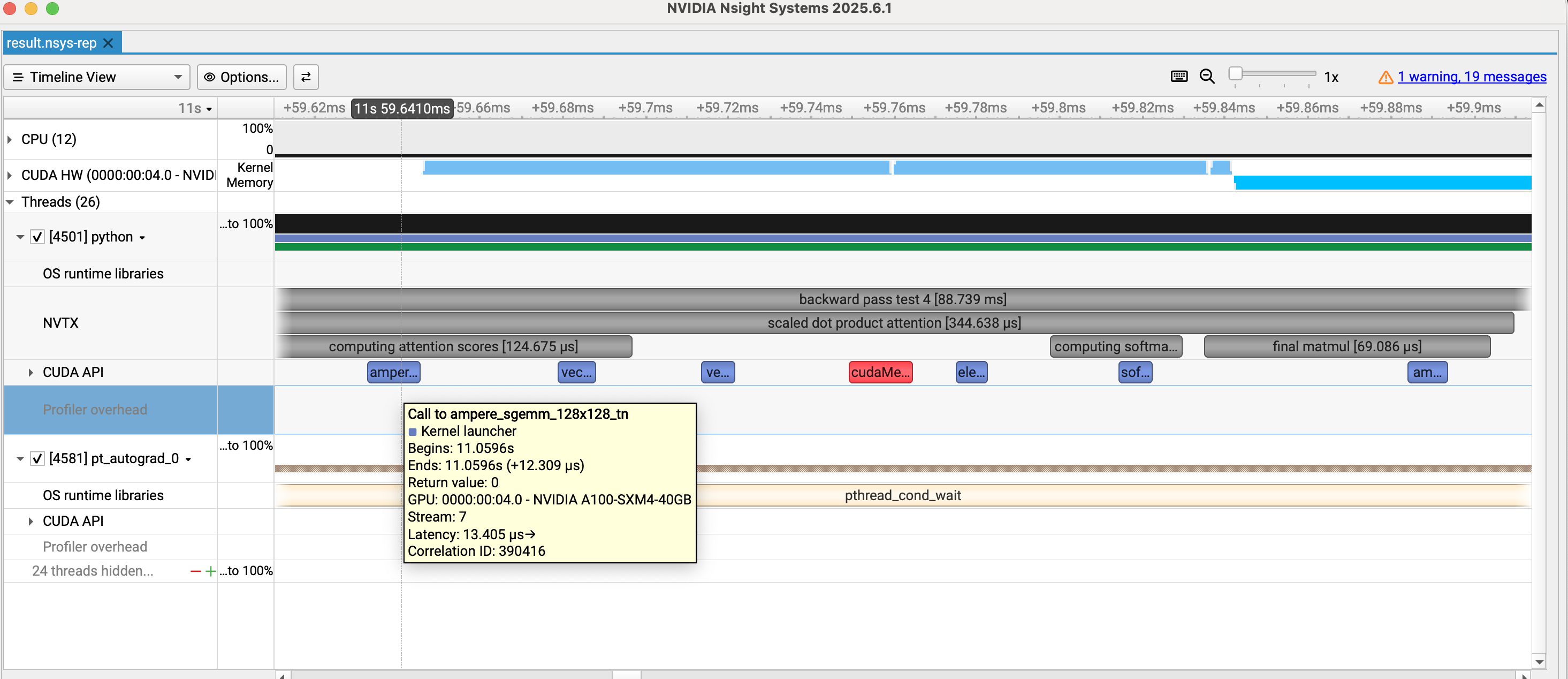
具体kernel的使用情况:
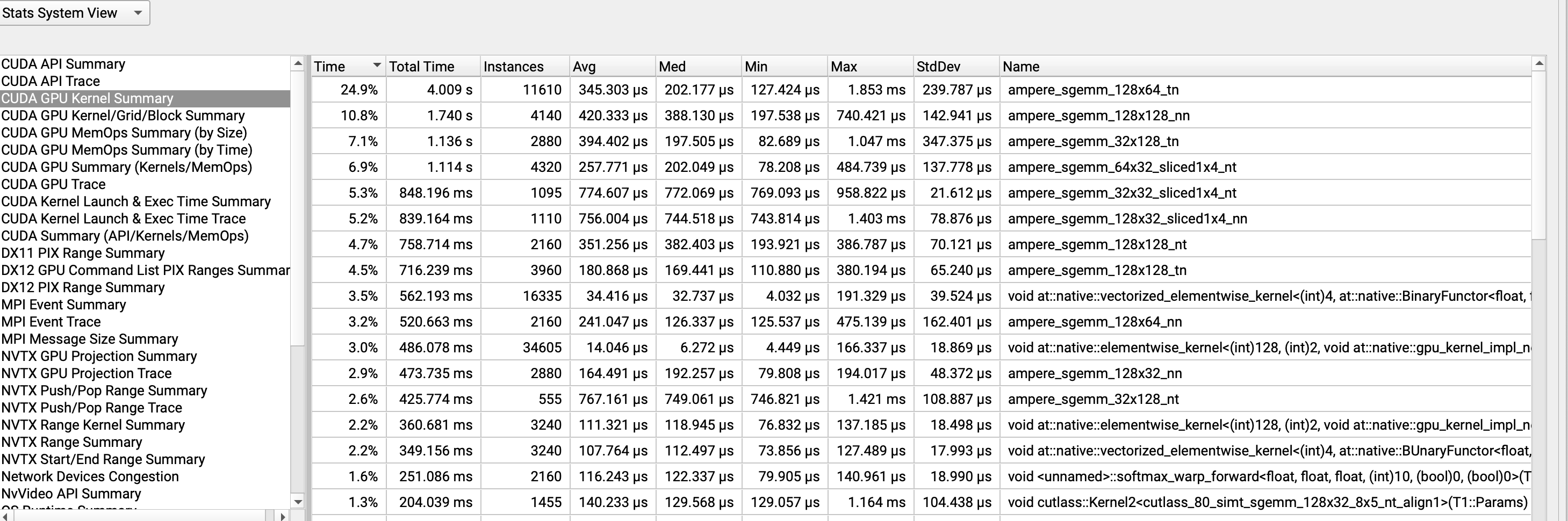
- 分析可以知道矩阵乘法的kernel 也就是sgemm_128这种是占比最多的,数字代表切分的不同大小的块,其次就是element-wise这种逐元素操作。
- 关于softmax操作相对于矩阵乘法优化不多,即计算量不大但所占用时间较多,性价比低。主要是memory bound问题。
3.精度问题
- 使用累加这种操作,需要高精度保存,使用autocast进行自动精度选择
- 矩阵乘法可以使用fp16,而加法以及layernorm这种则需要fp32,loss以及梯度值为了精准也要fp32
4.测量memory使用
# Start recording memory history.
5 torch.cuda.memory._record_memory_history(max_entries=1000000)
7... # what you want to profile in your benchmarking script
9 # Save a pickle file to be loaded by PyTorch's online tool.
10 torch.cuda.memory._dump_snapshot("memory_snapshot.pickle")
12 # Stop recording history.
13 torch.cuda.memory._record_memory_history(enabled=None)
5.torch.compile使用
- 时间消耗与seq_len成平方比,compile类c++提前编译运行优化。
FlashAttention2
2.用triton写flash attention的前向传播和反向传播?
推荐先看b站rethinkfun的视频过一遍:
https://www.bilibili.com/video/BV1UT421k7rA/?share_source=copy_web&vd_source=783046dd26b6d8ed3ae12d74958b0584
从高度上看,原先的attention计算由于要计算非常大S、 P中间变量矩阵,即(batch,nhead,seq,seq),这是非常大的矩阵,来回从HBM和SRAM中搬运很耗时间也就是IO 很慢。总体的解决方法:虽然增加了计算量 但io次数大大减小。
- tile 分块,online softmax
- backward时候recomputation
- kernel fusion
分别前向传播的算子和反向传播的算子,然后使用torch.autograd.Fuction类作为桥梁调用底层triton。
$\begin{aligned} \mathbf{S} & =\mathbf{Q}\mathbf{K}^\top/\sqrt{d} \ \mathbf{P}{ij} & =\mathrm{softmax}_j(\mathbf{S}){ij} \ \mathbf{O} & =\mathbf{P}\mathbf{V} \end{aligned}$
前向传播

根据前面triton的softmax基本可以入门了,triton会初始化每个program instance,里面包含了多个threads。这也是与cuda的一个区别,cuda面向的更具体的thread更精细复杂,而triton进行了封装更友好,面向block。
我们需要传入计算的指针地址,各个变量的stride,还有一些如seq dim scale等变量,以及一些常量tl.constexpr如tile size。
对于每个实例我们需要找到对应的query index,batch index,我们是处理哪一块索引。这里使用了tl.make_block_ptr更加智能的写法,而不用取手动算offset以及越界mask等。找到Q处理的具体块,然后遍历K V块。关键存储了l m这两个中间变量解决了softmax的一次次修正。l:每一行的exp sum,减去了max m修正的和。L:原本的log sum exp,用于反向传播优化。m:每一行的max。
需要有两次掩码,一次是我们需要的因果注意力掩码,另一次则是判断切分成块边界是否越界。
手册给出了一些优化tip:
# O_i = tl.exp(m_i_old - m_i)[:, None] * O_i + tl.dot(P_i, V_j)
# 优化版本(使用 acc)
O_i = tl.exp(m_i_old - m_i)[:, None] * O_i
O_i = tl.dot(P_i, V_j, acc=O_i) # 累积到 O_i
# 将 O_i 转换回原始数据类型(与 Q 相同),使用*_block_ptr.type.element_ty
tl.store(O_block_ptr, O_i.to(O_block_ptr.type.element_ty), boundary_check=(0, 1))
算法实现逻辑如上图,具体细节如下图代码:已经详细注释
# Kernel 3: Forward Pass
@triton.jit
def flash_fwd_kernel(
Q_ptr, K_ptr, V_ptr, # 输入指针
O_ptr, L_ptr,# 输出指针,L式logsumexp需要保存用于反向传播
stride_qb, stride_qq, stride_qd, # Q的stride,包括跳一个batch,跳一个query,跳一个dimension所需要的步长
stride_kb, stride_kk, stride_kd,
stride_vb, stride_vk, stride_vd,
stride_ob, stride_oq, stride_od,
stride_lb, stride_lq, # L的stride,二维tensor
N_QUERIES, N_KEYS, # 一般等于seq_len
scale, # 1/sqrt(d)
D: tl.constexpr, # d维度大小
Q_TILE_SIZE: tl.constexpr, # 每次处理的query块大小
K_TILE_SIZE: tl.constexpr, # 每次处理的key value块大小
is_causal: tl.constexpr # 是否是causal attention,需要掩码
):
query_tile_index = tl.program_id(0) # 第几个query块,第0维度并行性更好,用来划分query块
batch_index = tl.program_id(1) # 第几个batch,第1维度并行性较差,用来划分batch
# tl.make_block_ptr(
# base, # 基地址(指针)
# shape, # 整个张量的形状
# strides, # 步长(stride)
# offsets, # 块的起始位置
# block_shape, # 块的大小
# order # 内存布局顺序
# )
Q_block_ptr = tl.make_block_ptr(
Q_ptr + batch_index * stride_qb, # batch维度偏移,这个batch的起始位置
shape = (N_QUERIES, D), # Q的整体shape,即(seq_len, d),也是(N_QUERIES, D),用于边界检查
strides = (stride_qq, stride_qd),
offsets = (query_tile_index*Q_TILE_SIZE, 0), # 每个query块的起始位置
block_shape = (Q_TILE_SIZE, D), # 每个块的shape
order = (1, 0), # 内存布局顺序,遍历顺序,这里是d维度优先
)
K_block_ptr = tl.make_block_ptr(
K_ptr + batch_index * stride_kb,
shape = (N_KEYS, D),
strides = (stride_kk, stride_kd),
offsets = (0, 0), # K, V的offsets都应该从0开始,随j遍历是内循环
block_shape = (K_TILE_SIZE, D),
order = (1, 0),
)
V_block_ptr = tl.make_block_ptr(
V_ptr + batch_index * stride_vb,
shape = (N_KEYS, D),
strides = (stride_vk, stride_vd),
offsets = (0, 0),
block_shape = (K_TILE_SIZE, D),
order = (1, 0),
)
O_block_ptr = tl.make_block_ptr(
O_ptr + batch_index * stride_ob,
shape = (N_QUERIES, D),
strides = (stride_oq, stride_od),
offsets = (query_tile_index*Q_TILE_SIZE, 0),
block_shape = (Q_TILE_SIZE, D),
order = (1, 0),
)
L_block_ptr = tl.make_block_ptr(
L_ptr + batch_index * stride_lb,
shape = (N_QUERIES, ), # L是一维tensor,shape是(seq_len,)
strides = (stride_lq, ),
offsets = (query_tile_index*Q_TILE_SIZE,),
block_shape = (Q_TILE_SIZE,),
order = (0,), # 一维tensor只有一个维度
)
O_i = tl.zeros((Q_TILE_SIZE, D), dtype=tl.float32) # 需要初始化,注o数据类型
l_i = tl.zeros((Q_TILE_SIZE,), dtype=tl.float32)
m_i = tl.full((Q_TILE_SIZE,), -float("inf"), dtype=tl.float32) # tl.full的使用,-float("inf")
# 加载Q块,有边界检查
Q_i = tl.load(Q_block_ptr, boundary_check=(0, 1), padding_option="zero")
Q_i = tl.cast(Q_i, tl.float32) # 数据类型转换
for j in range(tl.cdiv(N_KEYS, K_TILE_SIZE)):
# j_start表示当前块在key维度的起始位置
j_start = j * K_TILE_SIZE
# 判断是否需要跳过这个块
should_skip = False
if is_causal:
q_max_idx = (query_tile_index + 1) * Q_TILE_SIZE - 1
k_min_idx = j_start
should_skip = q_max_idx < k_min_idx
if not should_skip:
# 创建 key index 向量并判断哪些是有效(< N_KEYS)
# 这两行代码的作用是创建有效性掩码(validity mask),用于处理序列长度不能被块大小整除的边界情况
# 具体来说:
# j=3, j_start = 3 * 32 = 96
# k_idx = tl.arange(0, 32) + 96
# k_idx = [96, 97, 98, 99, 100, 101, ..., 127]
# shape: (32,)
# N_KEYS = 100
# valid_k = k_idx < 100
# valid_k = [True, True, True, True, False, False, ..., False]
# (96-99 为 True,100-127 为 False)
# shape: (32,)
k_idx = tl.arange(0, K_TILE_SIZE) + j_start # shape (K_TILE_SIZE,)
valid_k = k_idx < N_KEYS # boolean mask shape (K_TILE_SIZE,)
K_j = tl.load(K_block_ptr, boundary_check=(0, 1), padding_option="zero")
V_j = tl.load(V_block_ptr, boundary_check=(0, 1), padding_option="zero")
K_j = tl.cast(K_j, tl.float32) # 数据类型
V_j = tl.cast(V_j, tl.float32)
S_i = tl.dot(Q_i, tl.trans(K_j)) * scale
# mask operation
if is_causal:
# 计算块中元素在S中的的行数
q_idx = tl.arange(0, Q_TILE_SIZE) + query_tile_index * Q_TILE_SIZE # shape (Q_TILE_SIZE,)
# 计算块中元素在S中的的列数
k_idx_tile = tl.arange(0, K_TILE_SIZE) + j_start # shape (K_TILE_SIZE,)
# 行数大于列数就被mask,合理利用广播机制
causal_mask = q_idx[:, None] >= k_idx_tile[None, :] # shape (Q_TILE_SIZE, K_TILE_SIZE)
# Key 位置 →
# k4 k5 k6 k7
# Query q4 [T, F, F, F] ← query 4 只能看到 key 4 (自己)
# 位置 q5 [T, T, F, F] ← query 5 可以看到 key 4-5
# ↓ q6 [T, T, T, F] ← query 6 可以看到 key 4-6
# q7 [T, T, T, T] ← query 7 可以看到 key 4-7
# 解释:
# q4 >= k4 → T, q4 >= k5 → F, q4 >= k6 → F, q4 >= k7 → F
# q5 >= k4 → T, q5 >= k5 → T, q5 >= k6 → F, q5 >= k7 → F
# q6 >= k4 → T, q6 >= k5 → T, q6 >= k6 → T, q6 >= k7 → F
# q7 >= k4 → T, q7 >= k5 → T, q7 >= k6 → T, q7 >= k7 → T
# Apply causal mask: add -1e6 to masked out elements
S_i = tl.where(causal_mask, S_i, S_i - 1e6)
# tl.where(condition, if_true, if_false)
# 如果 causal_mask[i, j] == True: 保持 S_i[i, j]
# 如果 causal_mask[i, j] == False: S_i[i, j] = S_i[i, j] - 1e6
# 广播应用:整列掩码
# valid_k[None, :] -> [1, K_TILE_SIZE]
# k96 k97 k98 k99 k100 k101 ... k127
# q0 [[ T, T, T, T, F, F, ... F], # 每列统一
# q1 [ T, T, T, T, F, F, ... F],
# q2 [ T, T, T, T, F, F, ... F],
# q3 [ T, T, T, T, F, F, ... F]]
S_i = tl.where(valid_k[None,:], S_i, -float("inf"))
m_i_old = m_i
m_i = tl.maximum(m_i_old, tl.max(S_i, axis=-1))
P_i = tl.exp(S_i - m_i[:, None]) # triton中不能用...,None
l_i = tl.exp(m_i_old - m_i) * l_i + tl.sum(P_i, axis=-1)
# O_i = tl.exp(m_i_old - m_i)[:, None] * O_i + tl.dot(P_i, V_j)
# 优化版本(使用 acc)
O_i = tl.exp(m_i_old - m_i)[:, None] * O_i
O_i = tl.dot(P_i, V_j, acc=O_i) # 累积到 O_i
K_block_ptr = K_block_ptr.advance((K_TILE_SIZE, 0)) # 相当于移动offset
V_block_ptr = V_block_ptr.advance((K_TILE_SIZE, 0))
O_i = O_i / l_i[:, None]
L_i = m_i + tl.log(l_i) # 真实的logsumexp值
# 将 O_i 转换回原始数据类型(与 Q 相同)
tl.store(O_block_ptr, O_i.to(O_block_ptr.type.element_ty), boundary_check=(0, 1))
tl.store(L_block_ptr, L_i.to(L_block_ptr.type.element_ty), boundary_check=(0,))
反向传播
$\begin{aligned} & \mathbf{S}=\mathbf{QK}^\top/\sqrt{d} \ \mathbf{P}{ij} & =\exp\left(\mathbf{S}{ij}-L_i\right) \ \mathrm{dV} & =\mathbf{P}^\top\mathbf{dO} \ \mathrm{dP} & =\mathbf{d}\mathbf{O}\mathbf{V}^\top \ \mathbf{dS}{ij} & =\mathbf{P}{ij}\circ(\mathbf{dP}_{ij}-D_i) \ \mathbf{d}\mathbf{Q} & =\mathbf{dSK}/\sqrt{d} \ \mathrm{dK} & =\mathbf{dS}^\top\mathbf{Q}/\sqrt{d}, \end{aligned}$

- 1.反向传播麻烦一点,这里分为了两个kernel计算,更容易理解。但是这样并行降低了效率,融为一个kernel 计算dQ dK dV更需要复杂的调度,效率会更高。
- 2.反向传播计算我们计算了一个D值,其实就是O·dO,这个提前计算好。
- 3.两个kernel的遍历顺序不同,一个是k v,一个是 q。避免 atomics,更好的内存访问模式
具体实现代码见仓库。
3.优化flashattention2
注意点:
- 在triton内核中,element shape应该是2的幂次方,如果不是的话需要padding到最小的2的次方来保证正常运行
- triton中间变量由于是初始为fp32,当处理bf16时候需要进行cast转换,tl.dot 要求两个操作数类型相同
- tl.store(dK_block_ptr, dK.to(dK_block_ptr.type.element_ty), boundary_check=(0, 1))
实验对比了两种 Flash Attention 实现:
我的colab实现完整优化测试结果链接:完整benchmark运行结果
- PyTorch 版本:使用 torch.nn.functional.scaled_dot_product_attention(PyTorch 内置的优化实现)
- Triton 版本:自己实现的 Flash Attention kernel
测试配置:
- GPU: NVIDIA A100-SXM4-80GB
- 序列长度: 128 ~ 65536
- 头维度 (d): 16, 32, 64, 128
- 数据类型: bfloat16, float32
- triton.testing.do_bench进行测试
tile size:固定16,16
结果选取:
Running benchmark: seq_len=16384, d=16, dtype=torch.float32
PyTorch: fwd=9.91ms, bwd=8.14ms, fwd+bwd=18.05ms
Triton: fwd=2.27ms, bwd=5.95ms, fwd+bwd=8.21ms
Speedup: fwd=4.37x, bwd=1.37x, fwd+bwd=2.20x
Running benchmark: seq_len=16384, d=32, dtype=torch.float32
PyTorch: fwd=10.29ms, bwd=8.73ms, fwd+bwd=19.02ms
Triton: fwd=3.05ms, bwd=7.47ms, fwd+bwd=10.50ms
Speedup: fwd=3.37x, bwd=1.17x, fwd+bwd=1.81x
Running benchmark: seq_len=16384, d=64, dtype=torch.float32
PyTorch: fwd=12.36ms, bwd=12.57ms, fwd+bwd=24.92ms
Triton: fwd=4.15ms, bwd=13.21ms, fwd+bwd=17.37ms
Speedup: fwd=2.98x, bwd=0.95x, fwd+bwd=1.43x
Running benchmark: seq_len=16384, d=128, dtype=torch.float32
PyTorch: fwd=16.05ms, bwd=20.05ms, fwd+bwd=36.09ms
Triton: fwd=8.18ms, bwd=27.51ms, fwd+bwd=35.68ms
Speedup: fwd=1.96x, bwd=0.73x, fwd+bwd=1.01x
Running benchmark: seq_len=32768, d=16, dtype=torch.float32
PyTorch: fwd=42.97ms, bwd=32.48ms, fwd+bwd=75.54ms
Triton: fwd=8.35ms, bwd=21.93ms, fwd+bwd=30.27ms
Speedup: fwd=5.15x, bwd=1.48x, fwd+bwd=2.50x
- 前向传播 Triton 版本普遍快 2-5 倍
- 随着 d增大,加速比下降
- 长序列时加速比反而更稳定
问题发现:
- 反向传播几乎没有加速,甚至更慢
- 特别是 [d=128] 时,Triton 反向比 PyTorch 慢
问题 1:Tile Size 太小
对于 A100 GPU:
- 共享内存:164 KB per SM
- 建议 tile size:64-128(Flash Attention 2 论文推荐)
问题 2:反向需要两个 kernel
实现分成了两个 kernel:
Kernel 1: flash_bwd_dq_kernel → 计算 dQ Kernel 2: flash_bwd_dk_dv_kernel → 计算 dK, dV
- 两次 kernel 启动开销
- 两次 遍历 Q, K, V
- 无法共享中间结果
优化tip:
• Tune the tile sizes for your kernel (use Triton autotune for this!)
• Tune additional Triton config parameters
• Implement the backward pass in Triton, not just torch.compile (see Section 1.3.4 below)
• Do two passes over your input for the backward pass, one for dQ and another for dK and dV to avoid
atomics or synchronization between blocks.
• Stop program instances early when doing causal masking, skipping all tiles that are always all zero
• Separate the non-masked tiles from the tile diagonals, computing the first without ever comparing
indices, and the second with a single comparison
• Use TMA (Tensor Memory Accelerator) functionality on H100, following a similar pattern to this
tutorial.
我们已经用triton实现backward了,优化朝着stop casual mask zero,autotune tile size and config,
以及将块分为上三角 对角 下三角分别优化,融为一个kernel等进阶操作。
优化1-使用skip causal zero
for j in range(tl.cdiv(N_KEYS, K_TILE_SIZE)):
j_start = j * K_TILE_SIZE
should_skip = False
if is_causal:
q_max_idx = (query_tile_index + 1) * Q_TILE_SIZE - 1
k_min_idx = j_start
should_skip = q_max_idx < k_min_idx
if not should_skip:
我们知道进行因果掩码时候,一般的上三角都会被掩码,也就是50%。而在分块实现中,比如q是第一块,而k v遍历所有的块,k v只有第一块才会进行计算,其余剩下的块就会被掩码,根本不用计算。所以当我们遇到这种情况,可以直接skip,可以提升50%左右,减少了50%的计算量。
注:triton不支持continue return等语句,triton不喜欢if else分支语句,但这里利大于弊。
使用“跳过全0块”(Skip Causal Zero)的实现显著优于未使用的版本,特别是在长序列任务中,性能提升接近 2 倍。
- 短序列 (Seq Len < 1024):两者差异不大,甚至由于逻辑判断开销,Skip 版本在极短序列下可能有微小的负优化(忽略不计)。
- 长序列 (Seq Len ≥ 8192):Skip 版本展现出巨大的优势。在序列长度达到 32k 或 64k 时,速度提升稳定在 1.7x 到 2.0x 之间。
- 原因核心:在 Causal Mask(因果遮罩/下三角掩码)场景下,注意力矩阵的一半(上三角部分)是无效的。Skip 机制在加载数据和计算前直接跳过了这 50% 的无效计算量。
结果部分:
Running benchmark: seq_len=32768, d=16, dtype=torch.float32
PyTorch: fwd=42.88ms, bwd=32.38ms, fwd+bwd=75.38ms
Triton: fwd=4.95ms, bwd=11.19ms, fwd+bwd=16.14ms
Speedup: fwd=8.67x, bwd=2.89x, fwd+bwd=4.67x
Running benchmark: seq_len=32768, d=32, dtype=torch.float32
PyTorch: fwd=44.39ms, bwd=34.23ms, fwd+bwd=78.74ms
Triton: fwd=6.84ms, bwd=14.50ms, fwd+bwd=21.33ms
Speedup: fwd=6.49x, bwd=2.36x, fwd+bwd=3.69x
Running benchmark: seq_len=32768, d=64, dtype=torch.float32
PyTorch: fwd=51.43ms, bwd=48.56ms, fwd+bwd=100.05ms
Triton: fwd=11.09ms, bwd=25.84ms, fwd+bwd=36.92ms
Speedup: fwd=4.64x, bwd=1.88x, fwd+bwd=2.71x
Running benchmark: seq_len=32768, d=128, dtype=torch.float32
PyTorch: fwd=65.61ms, bwd=77.04ms, fwd+bwd=142.69ms
Triton: fwd=20.49ms, bwd=51.13ms, fwd+bwd=71.80ms
Speedup: fwd=3.20x, bwd=1.51x, fwd+bwd=1.99x
Running benchmark: seq_len=65536, d=16, dtype=torch.float32
PyTorch: fwd=171.93ms, bwd=128.27ms, fwd+bwd=299.64ms
Triton: fwd=17.98ms, bwd=42.99ms, fwd+bwd=60.97ms
Speedup: fwd=9.56x, bwd=2.98x, fwd+bwd=4.91x
相比第一次,确实提升了1.7-2倍。
优化2- autotune tile size and config
在 Flash Attention 的场景下,16x16 通常太小了,会导致性能非常差。原因如下:
- 内存访问效率(Memory Coalescing): GPU 喜欢“大口吃肉”。从 HBM(全局显存)读取数据时,通常一次读取 128 字节。如果你的块太小(比如 16),每次读取的数据量少,但发出的读取指令次数多,会导致显存带宽利用率极低。
- 比喻:就像搬砖,用手推车(大块)一次搬一堆,比用勺子(小块)一次搬一点要快得多,哪怕勺子更灵活。
- Tensor Core 利用率: Triton 底层会调用 GPU 的 Tensor Core 进行矩阵乘法。Tensor Core 在处理较大的矩阵(如 M=64, N=64, K=32)时效率最高。16x16 往往填不满 Tensor Core 的流水线,导致计算单元空转。
- 循环开销(Loop Overhead): Block 越小,意味着切分的总块数越多,主循环的迭代次数就越多。循环本身的跳转、索引计算也是有开销的。
# 定义 autotune 的配置搜索空间
# 这会尝试不同的块大小、warp数量和流水线级数,找到性能最好的组合
def get_configs():
return [
# --- 方案A: 针对 bfloat16 + d<=64 的高性能配置 ---
# 显存消耗: 高 (stages=3 需要大量 SRAM)
triton.Config({'Q_TILE_SIZE': 128, 'K_TILE_SIZE': 64}, num_warps=8, num_stages=3),
triton.Config({'Q_TILE_SIZE': 64, 'K_TILE_SIZE': 64}, num_warps=4, num_stages=3),
triton.Config({'Q_TILE_SIZE': 128, 'K_TILE_SIZE': 32}, num_warps=4, num_stages=3),
# --- 方案B: 针对 bfloat16 + d=128 或 float32 + small d 的平衡配置 ---
# 显存消耗: 中 (stages=2 节省显存)
triton.Config({'Q_TILE_SIZE': 128, 'K_TILE_SIZE': 64}, num_warps=8, num_stages=2),
triton.Config({'Q_TILE_SIZE': 64, 'K_TILE_SIZE': 64}, num_warps=4, num_stages=2),
triton.Config({'Q_TILE_SIZE': 128, 'K_TILE_SIZE': 32}, num_warps=4, num_stages=2),
triton.Config({'Q_TILE_SIZE': 64, 'K_TILE_SIZE': 32}, num_warps=4, num_stages=2),
triton.Config({'Q_TILE_SIZE': 32, 'K_TILE_SIZE': 32}, num_warps=4, num_stages=2),
# --- 方案C: 针对 float32 + d=128 的"求生"配置 ---
# 显存消耗: 低 (stages=1 放弃流水线,只求不爆显存)
# 这里的 32x32 + stage=1 几乎可以适应任何苛刻环境
triton.Config({'Q_TILE_SIZE': 32, 'K_TILE_SIZE': 32}, num_warps=4, num_stages=1),
triton.Config({'Q_TILE_SIZE': 64, 'K_TILE_SIZE': 32}, num_warps=4, num_stages=1),
]
# -----------------------------------------------------------------------------
# Kernel 1: 计算 dQ
@triton.autotune(
configs=get_configs(),
key=['N_QUERIES', 'N_KEYS'], # 当 seq_len 变化时重新调优
)
····
# [修改点]:Grid 使用 lambda,根据 Autotune 选出的 META['Q_TILE_SIZE'] 动态计算
grid = lambda META: (triton.cdiv(N_QUERIES, META['Q_TILE_SIZE']), batch_size)
flash_fwd_kernel[grid](
添加 @triton.autotune 装饰器:在每个 Kernel (@triton.jit 之前) 添加该装饰器。
定义 Config 搜索空间:指定一系列候选的 Q_TILE_SIZE (BLOCK_M), K_TILE_SIZE (BLOCK_N), num_warps (线程束数量) 和 num_stages (流水线级数)。
修改 Kernel 调用方式:在 Python 包装类 (Flash_attention_triton) 中,移除手动计算 Tile Size 的逻辑,改用 lambda META: 动态计算 Grid。因为 Tile Size 现在由 Autotune 决定,并在运行时通过 META 字典传回。
num_warps(线程束数量)是什么?
-
定义:
在 CUDA/GPU 架构中,Warp 是最基本的执行单元,包含 32 个线程(Threads)。它们是“同进同退”的。
num_warps=4 意味着在这个 Triton Kernel 的一个 Block 中,你分配了 $4 \times 32 = 128$ 个线程来协同工作。
num_warps=8 意味着分配了 $8 \times 32 = 256$ 个线程。
-
作用与选择逻辑:
- 计算能力:线程越多,并行计算能力越强。
- 资源限制(寄存器压力):每个线程都需要寄存器(Register)来存局部变量。GPU 上的寄存器总数是有限的。Warps 越多,消耗的总寄存器越多。如果寄存器不够用,编译器会发生 “Register Spill”(把数据溢出到慢速内存),导致性能暴跌。
- 搭配关系:
- 大 Tile (128x64):计算量大,需要更多的工人和算力,所以通常搭配 8 Warps。
- 小 Tile (32x32):计算量小,4 个 Warps 甚至 2 个 Warps 就够了。如果强行用 8 Warps,反而会因为线程间同步和资源抢占变慢。
num_stages(流水线级数)是什么?
-
定义:
这是 Triton 编译器的一个高级优化特性,指的是 软件流水线(Software Pipelining) 的深度。它利用了 Ampere (A100/3090) 架构及以后的 异步拷贝(Async Copy) 技术。
-
作用(通俗解释):
想象你在炒菜(做计算):
- num_stages=1 (无流水线):去冰箱拿菜 -> 切菜 -> 炒菜 -> 再去冰箱拿下一个菜…(炒菜的时候,手和冰箱都是闲着的)。
- num_stages=2 (双缓冲):你在炒第一道菜的时候,助手正在切第二道菜。
- num_stages=3:你在炒第一道菜,助手A在切第二道菜,助手B已经去冰箱拿第三道菜了。
目的:掩盖显存读取的延迟。当计算单元(Tensor Core)在算 $Tile_i$ 时,数据加载单元(DMA)已经在预加载 $Tile_{i+1}$ 甚至 $Tile_{i+2}$ 到 SRAM 中了。
-
为什么选 3?
- Stage 越高,SRAM 消耗越大:Stage=3 意味着你需要在共享内存中开辟 3 块缓冲区来轮转数据。如果 Tile 很大(如 128x128)且 Stage 很大(如 5),SRAM 可能会爆显存(Shared Memory Limit),导致编译失败。
- 经验值:对于 Flash Attention,通常 2 到 4 是甜蜜点(Sweet Spot)。
- Stage=2 是保守选择。
- Stage=3 通常能获得更好的掩盖效果,且在 A100 上通常能塞进 SRAM。
- Stage > 4 往往提升有限,但会极大地增加 SRAM
结果选取:
Running benchmark: seq_len=32768, d=32, dtype=torch.bfloat16
PyTorch: fwd=48.23ms, bwd=34.46ms, fwd+bwd=82.55ms
Triton: fwd=2.42ms, bwd=6.14ms, fwd+bwd=8.55ms
Speedup: fwd=19.95x, bwd=5.61x, fwd+bwd=9.66x
Running benchmark: seq_len=32768, d=64, dtype=torch.bfloat16
PyTorch: fwd=55.28ms, bwd=48.80ms, fwd+bwd=103.97ms
Triton: fwd=4.42ms, bwd=11.35ms, fwd+bwd=15.10ms
Speedup: fwd=12.49x, bwd=4.30x, fwd+bwd=6.89x
Running benchmark: seq_len=32768, d=128, dtype=torch.bfloat16
PyTorch: fwd=69.61ms, bwd=77.19ms, fwd+bwd=146.45ms
Triton: fwd=11.98ms, bwd=307.97ms, fwd+bwd=319.70ms
Speedup: fwd=5.81x, bwd=0.25x, fwd+bwd=0.46x # 有问题
Running benchmark: seq_len=65536, d=16, dtype=torch.bfloat16
PyTorch: fwd=187.08ms, bwd=128.13ms, fwd+bwd=314.84ms
Triton: fwd=5.31ms, bwd=13.96ms, fwd+bwd=19.25ms
Speedup: fwd=35.24x, bwd=9.18x, fwd+bwd=16.36x
Running benchmark: seq_len=65536, d=32, dtype=torch.bfloat16
PyTorch: fwd=193.03ms, bwd=134.00ms, fwd+bwd=327.11ms
Triton: fwd=8.08ms, bwd=22.25ms, fwd+bwd=30.35ms
Speedup: fwd=23.88x, bwd=6.02x, fwd+bwd=10.78x
最高前向传播已经是35倍了,确实多线程束和多stage性能大幅度提升。
但块的选取和config的配置也是一个问题,有些反向传播还是依旧很慢,不同配置的块如何配置分到最好配置还需要进一步研究。
DDP
3.从零实现naive ddp并逐步优化?
基础:https://stanford-cs336.github.io/spring2025-lectures/?trace=var/traces/lecture_08.json
b站视频推荐: https://www.bilibili.com/video/BV1mm42137X8/?share_source=copy_web&vd_source=783046dd26b6d8ed3ae12d74958b0584
先进行基本通信原语的理解和实现,了解ddp,FSDP,TP,PP,SP等差别,其实本质上是按维度划分并行。
- 数据并行
- 模型并行
- pipeline
- tensor
-
zero1-2-3
- 最基础的torch distributeted使用
import torch.distributed as dist
def setup(rank, world_size, backend):
os.environ["MASTER_ADDR"] = "localhost"
os.environ["MASTER_PORT"] = "29100"
dist.init_process_group(backend=backend,rank=rank,world_size=world_size)
dist.all_reduce(parameter.grad, op=dist.ReduceOp.SUM, async_op=True)
# 确保所有进程同步后再清理
dist.barrier()
# 清理分布式进程组
dist.destroy_process_group()
# 获取rank world-size
self.rank = dist.get_rank()
self.world_size = dist.get_world_size()
- Naive DDP
最直观的实现(naive_ddp.py)非常简单:
- 所有 GPU 并行跑 Forward 和 Backward。
- Backward 结束后,所有 GPU 停下来。
- 对每一个参数(Parameter)触发
dist.all_reduce。 - 更新参数。
问题:1.一个个参数通信,通信多次,而每次启动通信都会开销。
2.这造成了严重的 GPU 闲置。在反向传播计算每一层梯度时,网络带宽是空闲的;而等到最后通信时,计算单元(CUDA Cores)又是空闲的。这就像做饭时,非要切完所有菜才开始烧水,而不是边切菜边烧水。
2.Flatten
直接将所有要通信的梯度展平为一个tensor,之后再恢复原来shape,这样只需要通信一次,效率更高
flattened_grads = torch._utils._flatten_dense_tensors(grads)
dist.all_reduce(flattened_grads, op=dist.ReduceOp.AVG,async_op=False)
unflattened_grad = torch._utils._unflatten_dense_tensors(flattened_grads, grads)
3.overlap 计算与通信的重叠,类似流水线
在 My_DDP 类中引入了 hook 机制。PyTorch 允许我们在参数梯度计算完成的瞬间触发回调:
# 伪代码逻辑
for param in model.parameters():
if param.requires_grad:
# 当某一层梯度算完,立即把这层丢出去通信
param.register_post_accumulate_grad_hook(self.sync_model_grad_async)
效果:反向传播是从最后一层(Layer N)向第一层(Layer 0)进行的。
- 当 Rank 算出 Layer N 的梯度时,立即启动 Layer N 的
all_reduce(异步)。 - Rank 继续计算 Layer N-1 的梯度。此时,Layer N 的数据正在网线上飞奔。
这种流水线(Pipelining)设计掩盖了通信延迟。
4.Bucketing:小包合并,带宽打满
上述两者的合并实现,并选择一个个桶的通信
单纯的 Overlap 有个致命伤:现代模型有成千上万个参数 Tensor。如果每个 Tensor(哪怕很小)都发一次 all_reduce,会因为频繁的 Kernel Launch 和网络握手(TCP/IB Overhead)导致 CPU 过载,带宽利用率极低。
解决方案:Bucketing (分桶) 我在 DDPBucketed 中实现了桶机制:
- 开辟一块连续内存(Bucket),例如 25MB,注意bubble。
- 反向传播时,梯度不直接发,而是先填入 Bucket。
- Bucket 填满后,将整个 Bucket
flatten拍扁成一个大 Tensor,一次性发出去。
# 代码片段:ddp_overlap_bucketed.py
def _grad_hook(self, param):
bucket_idx = self.param_to_bucket[param]
# 检查桶里的梯度是否都就绪了
if self._is_bucket_ready(bucket):
# 拍扁 -> 异步通信
self._start_bucket_communication(bucket_idx)
Insight:这是 latency(延迟)和 bandwidth(带宽)的权衡。Bucketing 牺牲了一点点即时性,换取了极高的吞吐量。
4.Optimizer State Sharding (ZeRO-1)
数据并行,为什么要让每张卡都存一份完整的优化器状态?
我在 ShardedOptimizer.py 中实现了类似 DeepSpeed ZeRO Stage 1 的逻辑:
- 切分:将总参数平均分配给不同的 Rank(Owner)。Rank 0 只负责更新参数 A,Rank 1 只负责更新参数 B。
- 更新:Rank 0 拿着 A 的梯度更新 A,维护 A 的 Optimizer State。Rank 1 对 A 没有任何操作,甚至不需要存 A 的状态。
- 广播:更新完后,Rank 0 将最新的 A 广播(Broadcast)给所有其他人
class ShardedOptimizer(torch.optim.Optimizer):
def __init__(self, params, optimizer, **kwargs):
self.rank = dist.get_rank()
self.world_size = dist.get_world_size()
super().__init__(params, kwargs)
self.optimizer = optimizer(self.local_param_group['params'], **kwargs) # 先准备好local_param_group,再实例化本地的optimizer
@torch.no_grad()
def step(self,closure=None, **kwargs):# 注意参数传递,这个closure
self.optimizer.step(closure, **kwargs)
for src_rank in range(self.world_size): # 一定注意broadcase的方法,源是谁,接收是谁
for param_group in self.param_groups:
for i, param in enumerate(param_group['params']):
if i % self.world_size == src_rank:
dist.broadcast(param.data,src=src_rank)
def add_param_group(self, param_group: Dict[str, Any]):
# 传入的 param_group 是一个字典,其中 'params' 键对应的是一个参数列表。我们需要遍历这个列表。
# self.param_groups: List[Dict[str, Any]] = []
# 需要考虑到传入的是多个param_group的情况
super().add_param_group(param_group) # 先保存一份完整的模型参数
local_param_group: Dict[str, Any] = {'params':[]} # 只需要存param,不需要存其他的,因为实例化的时候有**kwargs
for i, param in enumerate(param_group['params']):
if i % self.world_size == self.rank:
local_param_group['params'].append(param)
self.local_param_group = local_param_group
总结
- 不要让 GPU 等待:计算与通信的重叠(Overlap)是提升 GPU 利用率的关键。
- 系统开销不可忽视:频繁的小包通信会由 CPU 调度瓶颈导致性能下降,Bucketing 至关重要。
- 显存换通信:ZeRO 技术本质上是在用通信带宽换取显存空间,让单卡能训练更大的模型。
pytorch 分布式训练:
https://docs.pytorch.org/tutorials/beginner/dist_overview.html
这里给出的技巧:
When deciding what parallelism techniques to choose for your model, use these common guidelines:
- Use DistributedDataParallel (DDP), if your model fits in a single GPU but you want to easily scale up training using multiple GPUs.
- Use torchrun, to launch multiple pytorch processes if you are using more than one node.
- See also: Getting Started with Distributed Data Parallel
- Use FullyShardedDataParallel (FSDP2) when your model cannot fit on one GPU.
- See also: Getting Started with FSDP2
- Use Tensor Parallel (TP) and/or Pipeline Parallel (PP) if you reach scaling limitations with FSDP2.
- Try our Tensor Parallelism Tutorial
- See also: TorchTitan end to end example of 3D parallelism
ddp:
分发: 记得用 torchrun。
数据: 记得不同 Rank 吃不同数据。
同步: 记得只在 Update 前同步梯度,验证时要聚合 Loss。
保存: 记得只有 Rank 0 干杂活(打印/保存)。
实际训练代码参考:https://github.com/karpathy/build-nanogpt
FSDP:从 DDP 迁移到 FSDP2 的 CheckList
- 思维转变: 不再是“拥有模型”,而是“持有切片”。
- 初始化: 不要只包 Root Model,要先包 Submodules (Layers),再包 Root。
- 优化器: 必须在
fully_shard(model)之后 再初始化 Optimizer(因为要等参数变成 DTensor)。 - 保存模型: 使用
torch.distributed.checkpoint而不是简单的torch.save。
参考文档
- https://github.com/Sherlock1956/SimpleDDPImplementation/tree/

 RedNote
RedNote